Did you know that in the world of machine learning, the efficiency of Deep Learning (DL) models can be significantly boosted by a technique called quantization? Imagine reducing the computational burden of your neural network without sacrificing its performance. Just like compressing a large file without losing its essence, model quantization allows you to make your models smaller and faster. Let's dive into the fascinating concept of quantization and unveil the secrets of optimizing your neural networks for real-world deployment.
Before we dig in, readers should be familiar with neural networks and the basic concept of quantization, including the terms scale (S) and zero point (ZP). For readers who would like a refresher, this article and this article explains the broad concept and types of quantization.
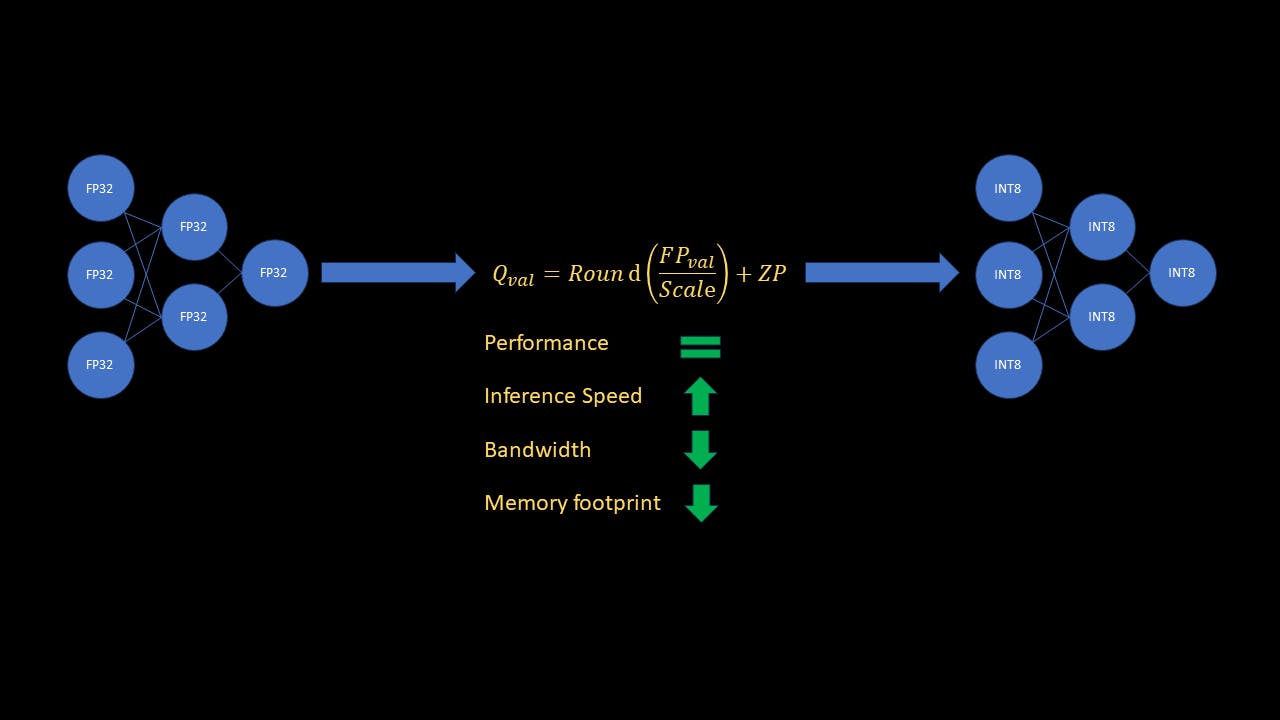
In this guide I will briefly explain why quantization matters, and how to implement it using Pytorch. I will focus mainly on the type of quantization called “post training static quantization”, which results in 4x lesser memory footprint of the ML model, and makes the inference up to 4x faster.
Concepts
Why Does Quantization Matter?
Neural Networks computations most commonly performed with 32 bit floating point numbers. A single 32 bit floating point number (FP32) requires 4 bytes of memory. In comparison, a single 8 bit integer number (INT8) only requires 1 byte of memory. Further, computers process integer arithmetic much faster than float operations. Right away, you can see that quantizing a ML model from FP32 to INT8 will result in 4x less memory. Further, it will also speed up inference by as much as 4x! With large models being all the rage right now, it is important for practitioners to be able to optimize trained models for memory and speed for real time inference.
Source- Tenor.com
Key Terms
-
Weights- Weights of the trained neural network.
-
Activations- In terms of quantization, activations are not the activation functions like Sigmoid or ReLU. By activations, I mean the feature map outputs of the intermediate layers, which are inputs to the next layers.
Post Training Static Quantization
Post training static quantization means we do not need to train or finetune the model for quantization after training the original model. We also do not need to quantize intermediate layer inputs, called activations on the fly. In this mode of quantization, the weights are directly quantized by computing the scale and zero point for each layer. For activations however, as the input to the model changes, the activations will change as well. We do not know the range of each and every input that the model will encounter during inference. So how can we compute the scale and zero point for all activations of the network?
We can do this by calibrating the model, using a good representative dataset. We then observe the range of values of activations for the calibration set, and then use those statistics to compute scale and zero point. This is done by inserting observers in the model, which collect data statistics during calibration. After preparing the model (inserting observers), we run the forward pass of the model on the calibration dataset. The observers use this calibration data to compute scale and zero point for activations. Now inference is only a matter of applying the linear transform to all layers with their respective scale and zero points.
While the entire inference is done in INT8, the final model output is dequantized (from INT8 to FP32).
Why do activations need to be quantized if the input and network weights are already quantized?
This is an excellent question. While the network input and weights are indeed already INT8 values, the output of the layer is stored as INT32, to avoid overflow. To reduce complexity in processing the next layer the activations are quantized from INT32 to INT8.
With the concepts clear, let’s dive into the code and see how it works!
For this example, I will use a resnet18 model fine-tuned on the Flowers102 dataset, available directly in Pytorch. However, the code will work for any trained CNN, with the appropriate calibration dataset. Since this tutorial is focused on quantization, I will not cover the training and fine-tuning part. However, all code can be found here. Lets dive in!
Quantization Code
Let us import the libraries necessary for quantization and to load the fine-tuned model.
import torch
import torchvision
import torchvision.transforms as transforms
from torchvision.models import resnet18
import torch.nn as nn
from torch.ao.quantization import get_default_qconfig
from torch.ao.quantization.quantize_fx import prepare_fx, convert_fx
from torch.ao.quantization import QConfigMapping
import warnings
warnings.filterwarnings('ignore')
Next, let us define some parameters, define data transforms and data loaders, and load the fine-tuned model
model_path = 'flowers_model.pth'
quantized_model_save_path = 'quantized_flowers_model.pth'
batch_size = 10
num_classes = 102
# Define data transforms
transform = transforms.Compose(
[transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize(
(0.485, 0.465, 0.406),
(0.229, 0.224, 0.225))]
)
# Define train data loader, for using as calibration set
trainset = torchvision.datasets.Flowers102(root='./data', split="train",
download=True, transform=transform)
trainLoader = torch.utils.data.DataLoader(trainset, batch_size=batch_size,
shuffle=True, num_workers=2)
# Load the finetuned resnet model
model_to_quantize = resnet18(weights=None)
num_features = model_to_quantize.fc.in_features
model_to_quantize.fc = nn.Linear(num_features, num_classes)
model_to_quantize.load_state_dict(torch.load(model_path))
model_to_quantize.eval()
print('Loaded fine-tuned model')
For this example, I will use some training samples as the calibration set.
Now, let us define the configuration used for quantizing the model.
# Define quantization parameters config for the correct platform,
# "x86" for x86 devices or "qnnpack" for arm devices
qconfig = get_default_qconfig("x86")
qconfig_mapping = QConfigMapping().set_global(qconfig)
In the above snippet, I have used the default config, but the QConfig class of Pytorch is used to describe how the model, or a part of the model should be quantized. We can do this by specifying the type of observer classes to be used to weights and activations.
We are now ready to prepare the model for quantization
# Fuse conv-> relu, conv -> bn -> relu layer blocks and insert observers
model_prep = prepare_fx(model=model_to_quantize,
qconfig_mapping=qconfig_mapping,
example_inputs=torch.randn((1,3,224,224)))
The prepare_fx function inserts the observers into the model, and also fuses conv→relu and conv→bn→relu modules. This results in lesser operations and lower memory bandwidth due to not needing to store intermediate results of those modules.
Calibrate the model by running forward pass on calibration data
# Run calibration for 10 batches (100 random samples in total)
print('Running calibration')
with torch.no_grad():
for i, data in enumerate(trainLoader):
samples, labels = data
_ = model_prep(samples)
if i == 10:
break
We don’t need to run calibration on the entire training set! In this example, I am using 100 random samples, but in practice, you should choose a dataset which is representative of what the model will see during deployment.
Quantize the model and save the quantized weights!
# Quantize calibrated model
quantized_model = convert_fx(model_prep)
print('Quantized model!')
# Save quantized
torch.save(quantized_model.state_dict(), quantized_model_save_path)
print('Saved quantized model weights to disk')
And that’s it! Now let us see how to load a quantized model, and then compare the accuracy, speed and memory footprint of the original and quantized models.
Load a quantized model
A quantized model graph is not quite the same as the original model, even if both have the same layers.
Printing the first layer (conv1) of both models shows the difference.
print('\nPrinting conv1 layer of fp32 and quantized model')
print(f'fp32 model: {model_to_quantize.conv1}')
print(f'quantized model: {quantized_model.conv1}')
1st layer of fp32 model and quantized model
You will notice that along with the different class, the quantized model’s conv1 layer also contains the scale and zero point parameters.
Thus, what we need to do it follow the quantization process (without calibration) to create the model graph, and then load the quantized weights. Of course, if we save the quantized model to onnx format, we can load it like any other onnx model, without running the quantization functions each time.
In the meantime, let us define a function for loading the quantized model and save it to inference_utils.py.
import torch
from torch.ao.quantization import get_default_qconfig
from torch.ao.quantization.quantize_fx import prepare_fx, convert_fx
from torch.ao.quantization import QConfigMapping
def load_quantized_model(model_to_quantize, weights_path):
'''
Model only needs to be calibrated for the first time.
Next time onwards, to load the quantized model,
you still need to prepare and convert the model without calibrating it.
After that, load the state dict as usual.
'''
model_to_quantize.eval()
qconfig = get_default_qconfig("x86")
qconfig_mapping = QConfigMapping().set_global(qconfig)
model_prep = prepare_fx(model_to_quantize, qconfig_mapping,
torch.randn((1,3,224,224)))
quantized_model = convert_fx(model_prep)
quantized_model.load_state_dict(torch.load(weights_path))
return quantized_model
Define functions for measuring accuracy and speed
Measure accuracy
import torch
def test_accuracy(model, testLoader):
model.eval()
running_acc = 0
num_samples = 0
with torch.no_grad():
for i, data in enumerate(testLoader):
samples, labels = data
outputs = model(samples)
preds = torch.argmax(outputs, 1)
running_acc += torch.sum(preds == labels)
num_samples += samples.size(0)
return running_acc / num_samples
This is a pretty straightforward Pytorch code.
Measure inference speed in milliseconds (ms)
import torch
from time import time
def test_speed(model):
dummy_sample = torch.randn((1,3,224,224))
# Average out inference speed over multiple iterations
# to get a true estimate
num_iterations = 100
start = time()
for _ in range(num_iterations):
_ = model(dummy_sample)
end = time()
return (end-start)/num_iterations * 1000
Add both these functions in inference_utils.py. We are now ready to compare models. Let us go through the code.
Compare models for accuracy, speed, and size
Let us first import necessary libraries, define parameters, data transforms, and the test dataloader.
import os
import torch
import torch.nn as nn
import torchvision
from torchvision.models import resnet18
import torchvision.transforms as transforms
from inference_utils import test_accuracy, test_speed, load_quantized_model
import copy
import warnings
warnings.filterwarnings('ignore')
model_weights_path = 'flowers_model.pth'
quantized_model_weights_path = 'quantized_flowers_model.pth'
batch_size = 10
num_classes = 102
# Define data transforms
transform = transforms.Compose(
[transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize(
(0.485, 0.465, 0.406),
(0.229, 0.224, 0.225))]
)
testset = torchvision.datasets.Flowers102(root='./data', split="test",
download=True, transform=transform)
testLoader = torch.utils.data.DataLoader(testset, batch_size=batch_size,
shuffle=False, num_workers=2)
Load the two models
# Load the finetuned resnet model and the quantized model
model = resnet18(weights=None)
num_features = model.fc.in_features
model.fc = nn.Linear(num_features, num_classes)
model.load_state_dict(torch.load(model_weights_path))
model.eval()
model_to_quantize = copy.deepcopy(model)
quantized_model = load_quantized_model(model_to_quantize,
quantized_model_weights_path)
Compare models
# Compare accuracy
fp32_accuracy = test_accuracy(model, testLoader)
accuracy = test_accuracy(quantized_model, testLoader)
print(f'Original model accuracy: {fp32_accuracy:.3f}')
print(f'Quantized model accuracy: {accuracy:.3f}\n')
# Compare speed
fp32_speed = test_speed(model)
quantized_speed = test_speed(quantized_model)
print(f'Inference time for original model: {fp32_speed:.3f} ms')
print(f'Inference time for quantized model: {quantized_speed:.3f} ms\n')
# Compare file size
fp32_size = os.path.getsize(model_weights_path)/10**6
quantized_size = os.path.getsize(quantized_model_weights_path)/10**6
print(f'Original model file size: {fp32_size:.3f} MB')
print(f'Quantized model file size: {quantized_size:.3f} MB')
Results
Comparison of fp32 vs quantized model
As you can see, the accuracy of the quantized model on the test data is almost as much as the accuracy of the original model! Inference with the quantized model is ~3.6x faster (!) and the quantized model requires ~4x lesser memory than the original model!
Conclusion
In this article, we understood the broad concept of ML model quantization, and a type of quantization called Post Training Static Quantization. We also looked at why quantization is important and a powerful tool in the time of large models. Finally, we went through example code to quantize a trained model using Pytorch, and reviewed the results. As the results showed, quantizing the original model did not impact performance, and at the same time decreased inference speed by ~3.6x and lowered the memory footprint by ~4x!
A few points to note- Static quantization works well for CNNs, but dynamic quantization is the preferred method for sequence models. Additionally, if quantization drastically impacts model performance, the accuracy can be regained by a technique called Quantization Aware Training (QAT).
How do Dynamic Quantization and QAT work? Those are posts for another time. I hope with this guide, you are provided the knowledge to perform static quantization on your own Pytorch models.
References